Empezamos la penúltima sesión del curso haciendo un repaso de lo que se ha explicado hasta ahora de la aplicación de la transformada de Laplace en los circuitos. A simple vista, parece que ya está todo explicado sobre el tema, pero si nos fijamos atentamente, veremos que hemos pasado por alto la duración del transitorio.
¿Cuál es la duración del transitorio?
Para encontrar aproximadamente la duración del transitorio, tenemos varias formas:
- Hacer el inverso de lo que acompaña a t en cada expresión del transitorio
- Hacer el inverso del ancho de banda
¿Cómo saber si un circuito es estable?
1) Obteniendo la H(s)
- Si es de 1er grado el denominador debe ser completo y de mismo signo en todos los factores
- Si es de 2do grado el denominador debe ser completo y de mismo signo en todos los factores
- Si es de 3er grado el denominador debe cumplir a2·a1>a3·a0
Excitaciones no periódicas ni uniformes
Para terminar la clase vamos a ver que sucede cuando excitamos un circuito con una excitación que no es ni periódica ni uniforme. Como este tipo de excitación no responde a ningún patrón repetitivo, la única forma de conocer lo que va a suceder es obteniendo valores discretos, lo que se llama discretizar una función. Para discretizar una función debemos conocer el intervalo de tiempo Ts, cuyo criterio es:
En el caso de simuladores de circuitos como PSPICE, el comando que representa el transitorio exige conocer el tiempo de discretización. El comando de los siguientes cuatro parámetros:
También tenemos un criterio llamado de Nyquistiv que establece la frecuencia mínima a la que se deben tomar muestras en una señal para no perder información. Este criterio esta basado en la siguiente expresión:
El procesado numérico de señal está relacionado con la discretización de una función y tiene utilidad para conocer la respuesta de un circuito sin necesidad de montarlo, simplemente usando algoritmos matemáticos. El proceso que se sigue es el mostrado en la imagen.
En el caso de simuladores de circuitos como PSPICE, el comando que representa el transitorio exige conocer el tiempo de discretización. El comando de los siguientes cuatro parámetros:
.TRAN (algo menor que el transitorio) (durada del transitorio) (0) (Ts)
También tenemos un criterio llamado de Nyquistiv que establece la frecuencia mínima a la que se deben tomar muestras en una señal para no perder información. Este criterio esta basado en la siguiente expresión:
Procesado numérico de señal
El procesado numérico de señal está relacionado con la discretización de una función y tiene utilidad para conocer la respuesta de un circuito sin necesidad de montarlo, simplemente usando algoritmos matemáticos. El proceso que se sigue es el mostrado en la imagen.

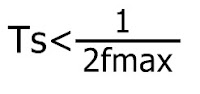

No comments:
Post a Comment